Em qual valor a parábola cruza o eixo y *?

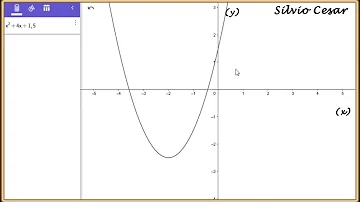
Em qual valor a parábola cruza o eixo y *?

INTERSEÇÃO DA PARÁBOLA COM O EIXO Y (EIXO DAS ORDENADAS): A parábola intercepta o eixo das ordenadas sempre quando temos o valor de x igual a zero, ou seja, y = a. 02 + b. 0 + c = 0 + 0 + c = c. Logo, a parábola intercepta o eixo das ordenadas no ponto (0,c).

Como determinar as interseções da parábola com o eixo xeo eixo y?

A parábola intersecta o eixo das abscissas (x) e o eixo das ordenadas (y). Dada uma função do 2º grau representada pela expressão y = ax² + bx + c, para descobrirmos se a parábola intersecta eixo x, devemos fazer y = 0 e resolver a equação do 2º grau com base na expressão ax² + bx + c = 0.

Onde a função corta o eixo y?

O ponto no qual a parábola cortará o eixo Oy dependerá do valor do coeficiente c, ou seja, se c = 2 isso significa que a parábola irá cortar o eixo Oy no ponto de coordenada 2.

Como descobrir onde a parábola corta o eixo y?

Se c>0, a parábola irá cortar o eixo Y acima da origem; Se c

Como encontrar o eixo y?

O eixo x é a linha horizontal onde o valor de y é igual a zero e o eixo y é a linha vertical onde o valor de x é igual a zero. O ponto onde a função intercepta o eixo y pode ser facilmente encontrado sabendo que, nesse ponto, x é igual a zero.

Como resolver vértice da parábola?

Esse ponto de retorno da parábola, mais conhecido como vértice da parábola, pode ser calculado com base nas expressões matemáticas envolvendo os coeficientes da função do 2º grau dada pela lei de formação y = ax² + bx + c.

Como achar o eixo de simetria de uma função quadrática?

Para calcular o eixo de simetria de um polinômio de segunda ordem na forma ax2 + bx +c (uma parábola), use a fórmula x = -b / 2a. No exemplo acima, a = 2 b = 3 e c = -1. Substitua os valores e você encontrará: x = -3 / 2(2) = -3/4.

Como achar o eixo da parábola?

O eixo de simetria de uma parábola é uma reta perpendicular à diretriz que passa pelo seu vértice. Consequentemente, essa reta também passa pelo foco da parábola e contém o segmento chamado parâmetro. Essas equações são obtidas colocando o vértice de uma parábola na origem de um plano cartesiano.

Qual é o eixo XEOY?

As duas retas numéricas usadas para determinar o plano cartesiano recebem o nome de eixos. A reta horizontal é chamada de eixo x, ou eixo das abscissas, e a reta vertical é chamada de eixo y, ou eixo das ordenadas.

Qual o valor da parábola?

• Dessa forma, a parábola não possui ponto de intersecção no eixo das abscissas. A parábola sempre intersectará o eixo das ordenadas (y) de acordo com o valor do coeficiente c da equação do 2º grau. Para determinarmos o valor do coeficiente c, basta atribuirmos a x, valor igual a zero.

Qual a segunda condição da parábola?

• Terceira condição: Quando Δ < 0, a função não possui raiz real; logo, a parábola não intercepta o eixo x. O que determina a concavidade da parábola é o coeficiente a da função de segundo grau – f (x) = a x 2 + bx + c.

Qual a concavidade da parábola?

• Nesse momento devemos levar em consideração a concavidade da parábola, ou seja, quando o coeficiente a > 0: concavidade para cima, e a < 0: concavidade para baixo. Não pare agora... Tem mais depois da publicidade ;)

Quais são os pontos notáveis de uma parábola?

• Podemos destacar em uma parábola três pontos notáveis, ou seja, com esses pontos podemos construir com mais facilidade um gráfico de uma função do 2ª grau. Eles se dividem em: pontos de intersecção da parábola com o eixo Ox, pontos de intersecção da parábola com o eixo Oy e vértices da parábola.