Para que serve o teorema fundamental da Álgebra?

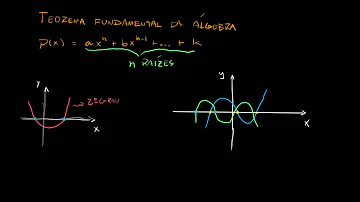
Para que serve o teorema fundamental da Álgebra?

Em matemática, o teorema fundamental da Álgebra afirma que qualquer polinômio p(z) com coeficientes complexos de uma variável e de grau �� ≥ 1 tem alguma raiz complexa.

O que diz um teorema?

Teorema é uma dedução lógica que pode ser provada a partir de deduções baseadas em axiomas (ou postulados). Ou seja, é o desdobramento de outros conceitos matemáticos considerados incontestáveis. O teorema precisa ser demonstrado — e essa demonstração pode ocorrer por outros teoremas.

O que o teorema fundamental da Álgebra fala sobre toda equação polinomial?

O teorema fundamental da álgebra (TFA), provado por Gauss em 1799, afirma que toda equação polinomial da seguinte forma possui pelo menos uma raiz complexa. A raiz de uma equação polinomial é sua solução, ou seja, o valor da incógnita é que torna a igualdade verdadeira.

O que é o teorema fundamental da aritmética?

Teorema fundamental da aritmética. Todo o número natural pode ser escrito como produto de números primos. Esse produto é único a menos da ordem dos fatores.

Qual é o teorema de d'Alembert?

O Teorema de D'Alembert facilita o cálculo da divisão de um polinômio por um binômio. ... O matemático francês D'Alembert provou, levando em consideração o teorema citado acima, que um polinômio qualquer Q(x) será divisível por x – a, ou seja, o resto da divisão será igual à zero (R = 0) se P(a) = 0.

Por que este teorema é inadequado para a álgebra?

• Este teorema é hoje em dia considerado inadequado por muitos matemáticos, por não ser fundamental para a álgebra contemporânea. Outras tentativas foram levadas a cabo por Euler (1749), de Foncenex (1759), Lagrange (1772) e Laplace (1795).

Quais são os elementos pertencentes à álgebra?

• Expressões algébricas, monômios e polinômios são exemplos de elementos pertencentes à álgebra, pois são constituídos a partir de operações realizadas com números desconhecidos. Lembre-se de que um número desconhecido pode representar qualquer número de um conjunto numérico.

Quando foi publicada a primeira demonstração da álgebra?

• A outra demonstração foi publicada por Gauss em 1799 e era sobretudo geométrica, mas tinha uma falha topológica. Uma demonstração rigorosa foi publicada por Argand em 1806; foi aqui que, pela primeira vez, o teorema fundamental da Álgebra foi enunciado para polinômios com coeficientes complexos e não apenas para polinómios com coeficientes reais.

Qual a parte da álgebra clássica?

• Os conceitos relacionados até aqui compõem a álgebra clássica. Essa parte da álgebra está mais ligada aos conjuntos dos números naturais, inteiros, racionais, irracionais, reais e complexos e é estudada tanto no ensino fundamental quanto no ensino superior.